Tree

Tree

트리 자료구조

트리는 노드 들이 나무가지처럼 연결된 비선형적 자료구조이다.

선형적 자료구조는 하나의 자료 뒤에 하나의 자료가 존재한다.

자료들간의 앞과 뒤 관계가 1대 1인 경우를 선형적이라고 얘기한다.

비선형은 그렇지 않은 경우라고 생각하면 편할 것 같다.

트리의 이미지를 보면, 한 눈에 보기에도 비선형적 자료구조라는 것을 알 수 있다.

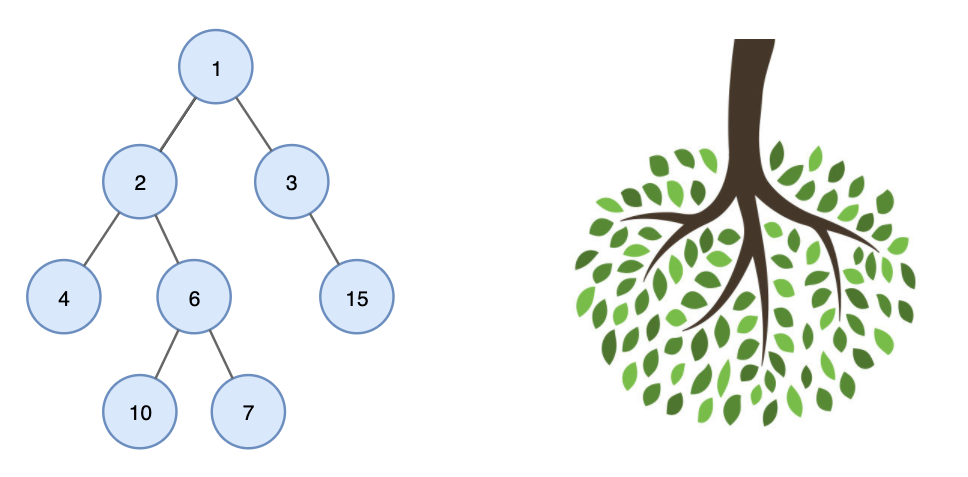
마찬가지로 하나의 트리가 또 다른 트리를 포함할 수 있으며, 이는 재귀적 자료구조라고 볼 수 있다.

트리의 용어

트리 구조에서 주로 사용하는 몇 가지 용어가 존재한다.

자주 쓰는 용어들만 정리하자면 다음과 같다.

Node: 트리를 구성하는 기본 요소

Edge: Node와 Node간의 연결 선

Root Node: 트리 구조에서 부모가 없는 최상위 Node

Parent Node: Child를 가지는 Node

Child Node: Parent Node의 하위 Node

Sibling Node: 같은 Parent를 공유하는 Node

External Node == Terminal Node == Leaf Node: Child가 없는 Node

Internal Node == Non-Terminal Node == Branch Node: Child를 하나 이상 가지는 Node

트리의 특징

다음은 트리의 특징을 정리한 것이며, 이에 위배될 경우 트리 자료구조라고 할 수 없다.

• 하나의 루트노드와 0개 이상의 하위 노드로 구성
• 데이터를 순차적으로 저장하지 않는 비선형적 자료구조
• 트리내에 또 다른 트리가 있는 재귀적 자료구조
• 무방향 그래프 구조
• 자식 노드는 하나의 부모노드만을 가진다
• 노드가 N개인 트리는 N-1개의 간선을 가진다

이진트리 구현

# header

typedef struct BinTreeNodeType
{
    char data;
    int visited;
    struct BinTreeNodeType    *pLeftChild;
    struct BinTreeNodeType    *pRightChild;
} BinTreeNode;

typedef struct BinTreeType
{
    struct BinTreeNodeType* pRootNode;
} BinTree;

#include "./bintree.h"

BinTree        *makeBinTree(BinTreeNode rootNode)
{
    BinTree        *newTree = calloc(1, sizeof(BinTree));
    BinTreeNode    *root = calloc(1, sizeof(BinTreeNode));

    root->data = rootNode.data;
    root->visited = 0;
    newTree->pRootNode = root;
    return (newTree);
}

BinTreeNode    *getRootNodeBT(BinTree *pBinTree)
{
    if (!pBinTree)
        return  (NULL);
    printf("root node data = %c\n", pBinTree->pRootNode->data);
    return (pBinTree->pRootNode);
}

// 부모노드에 자식 노드를 왼쪽에 넣어주고 자식노드를 리턴
BinTreeNode    *insertLeftChildNodeBT(BinTreeNode *pParentNode, BinTreeNode element)
{
    if (!pParentNode)
        return (NULL);
    BinTreeNode    *newNode = calloc(1, sizeof(BinTreeNode));
    newNode->data = element.data;
    newNode->visited = 0;
    pParentNode->pLeftChild = newNode;
    return (newNode);
}

// 부모노드에 자식 노드를 오른쪽에 넣어주고 자식노드를 리턴
BinTreeNode    *insertRightChildNodeBT(BinTreeNode *pParentNode, BinTreeNode element)
{
    if (!pParentNode)
        return (NULL);
    BinTreeNode    *newNode = calloc(1, sizeof(BinTreeNode));
    newNode->data = element.data;
    newNode->visited = 0;
    pParentNode->pRightChild = newNode;
    return (newNode);
}

// 노드의 왼쪽 자식노드를 리턴
BinTreeNode    *getLeftChildNodeBT(BinTreeNode *pNode)
{
    if (!(pNode->pLeftChild))
        return (NULL);
    return (pNode->pLeftChild);
}

// 노드의 오른쪽 자식노드를 리턴
BinTreeNode    *getRightChildNodeBT(BinTreeNode* pNode)
{
    if (!(pNode->pRightChild))
        return (NULL);
    return (pNode->pRightChild);
}

// 노드 하나를 삭제 
void    deleteBinTreeNode(BinTreeNode* pNode)
{
    pNode->pLeftChild = NULL;
    pNode->pRightChild = NULL;
    free(pNode);
}

// 트리 전체를 삭제
void    deleteBinTree(BinTree *pBinTree)
{
    if (!pBinTree)
        return ;
    free_leafNode(pBinTree->pRootNode);
    free(pBinTree);
}

void    free_leafNode(BinTreeNode *parentNode)
{
    if (parentNode->pLeftChild)
        free_leafNode(parentNode->pLeftChild);
    if (parentNode->pRightChild)
        free_leafNode(parentNode->pRightChild);
    free(parentNode);
}